Como fazer multiplicação ✖
Para encontrar o resultado da multiplicação, é necessário conhecer a tabuada e aprender a aplicar o algoritmo dessa operação quando necessário. Existem propriedades importantes na multiplicação, a saber:
propriedade comutativa;
propriedade distributiva;
propriedade associativa;existência de um elemento neutro; e
existência do inverso de um número.
Representação da multiplicação
![A multiplicação é uma operação básica da Matemática.[1]](https://static.mundoeducacao.uol.com.br/mundoeducacao/2021/04/multiplicacao.jpg)
A multiplicação é uma operação que utilizamos para facilitar o calculo da adição sucessiva de um número por ele mesmo. Por exemplo:
5 + 5 + 5 + 5 + 5 + 5 + 5 = 35
A adição sucessiva de 5 por ele mesmo 7 vezes pode ser representada de forma mais simples, a saber:
5 × 7 = 35
Chamamos o símbolo × de vezes, ou seja, estamos calculando 5 vezes 7. A multiplicação serve para facilitar a notação de adições sucessivas de um número por ele mesmo.
Termos da multiplicação
Em uma multiplicação, cada termo recebe um nome.
Fatores: os números que estamos multiplicando.
Produto: o resultado da multiplicação.
Exemplo:
3 × 7 = 21
3 e 7 → fatores
21 → produto
Para encontrar o produto entre dois números menores ou iguais a 10, utilizamos a tabuada:
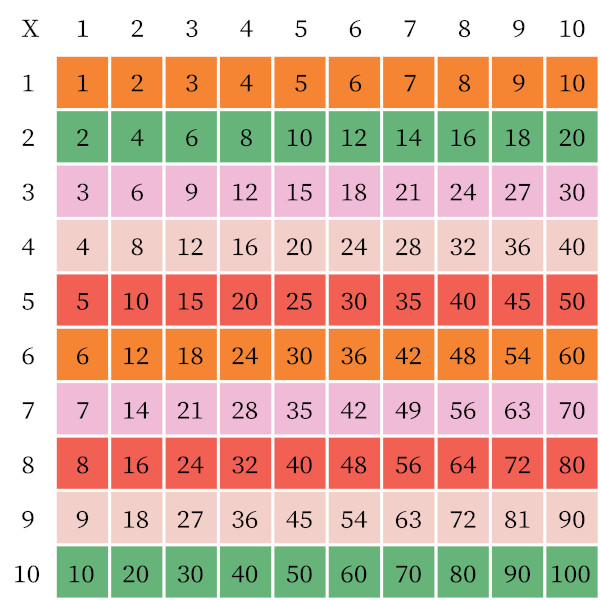
Quando queremos calcular a multiplicação entre dois números e pelo menos um deles não está na tabuada, ou seja, é maior do que 10, utilizamos o algoritmo da multiplicação, que será apresentado a seguir.
Veja também: Como calcular a multiplicação de números decimais?
Como fazer a multiplicação?
Quando o produto da multiplicação não está na tabuada, é necessário utilizar o algoritmo da multiplicação. Vamos compreender seu funcionamento por meio dos exemplos a seguir.
Exemplo 1:
Começando com um exemplo mais simples, vamos calcular 21 × 3.
Primeiramente montamos o algoritmo, colocando o número com maior quantidade de dígitos primeiro, conforme a demonstração a seguir:
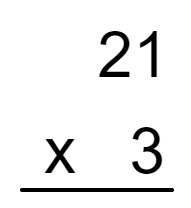
Agora realizamos a multiplicação entre as unidades, ou seja, 3 x 1 = 3. O resultado será colocado abaixo do 3.
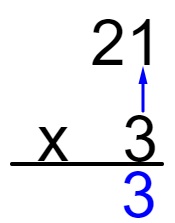
Agora vamos multiplicar a dezena do primeiro fator com a unidade do segundo fator, ou seja, 2 × 3 = 6, e o resultado será colocado na frente do primeiro resultado.
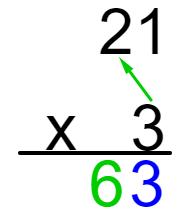
Então, o produto de 21 × 3 = 63.
Exemplo 2:
Agora faremos um caso um pouco mais complexo, quando a multiplicação entre as unidades resulta em um número maior que 9. Vamos calcular 43 × 6.
Montando o algoritmo:
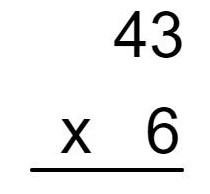
Realizando a multiplicação entre as unidades, sabemos que 6 × 3 = 18. Nesse caso, vamos colocar o 8 no produto e o 1 acima da casa das dezenas para somar com o próximo resultado.
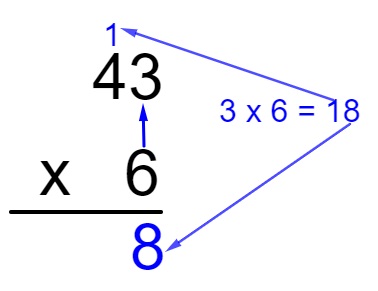
Agora realizaremos a segunda multiplicação, somando 1 ao seu resultado, ou seja, 6 × 4 + 1 = 24 + 1 = 25. Como não há mais nem um número no primeiro fator, vamos escrever 25 no produto.
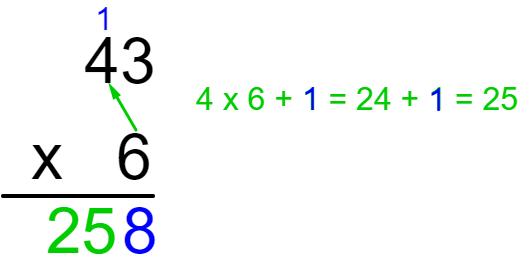
Então, 43 × 6 = 258.
Exemplo 3:
Agora faremos um exemplo em que os dois fatores são maiores que 9:
35 × 24
Para realizar essa multiplicação, vamos montar o algoritmo:
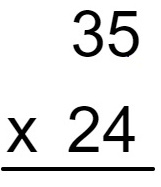
Agora multiplicaremos as unidades 4 x 5.
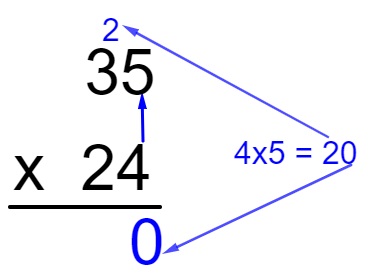
Faremos também a multiplicação de 4 x 3 e somaremos 2:
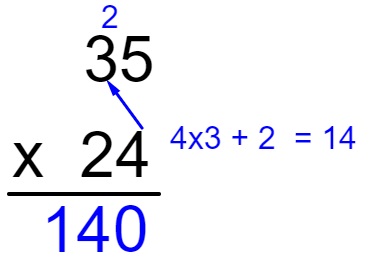
Agora vamos multiplicar a dezena do fator que está embaixo com a unidade do fator que está em cima. Como ele é uma dezena, 2 x 5 = 10.
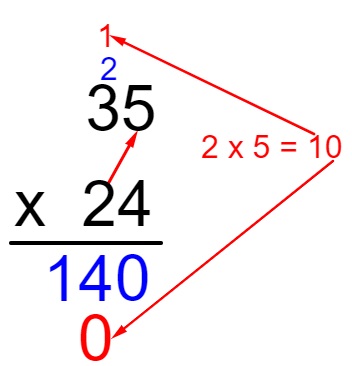
Como 2 é uma dezena, pulamos a casa das unidades ao escrever o 0. Agora multiplicaremos as dezenas dos dois fatores e somaremos 1, ou seja, 2 x 3 + 1 = 7.
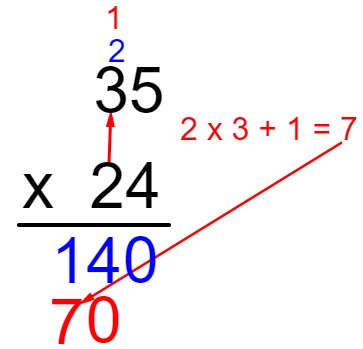
Agora vamos somar os resultados encontrados:
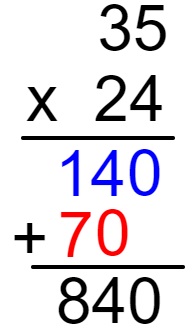
Leia também: 3 erros comuns ao resolver expressões numéricas
Propriedades da multiplicação
A multiplicação possui propriedades importantes, a saber: propriedade comutativa, distributiva, associativa, existência de um elemento neutro e existência do inverso de um número.
Propriedade comutativa
Em uma multiplicação, a ordem dos fatores não altera o produto.
a × b = b × a
Exemplo:
5 × 3 = 3 × 5 = 15
Propriedade distributiva
Conhecida informalmente como chuveirinho, essa propriedade envolve a adição e a multiplicação:
a ( b + c ) = ab + ac
Exemplo:
Vamos resolver a expressão:
4 ( 5 + 6)
Pela propriedade distributiva, existem dois caminhos possíveis para resolver essa expressão numérica. Por um caminho, podemos somar e depois realizar a multiplicação.
4 (5 + 6)
4 (11)
44
Pelo outro, podemos realizar a multiplicação de 4 por cada um dos termos, ou seja:
4 (5 + 6)
4 × 5 + 4 × 6
20 + 24
44
Propriedade associativa
A associação entre os termos vai gerar o mesmo produto:
(a × b) × c = a × (b × c)
Exemplo:
(2 × 3) × 4 = 2 × (3 × 4)
6 × 4 = 2 × 12
24 = 24
Note que a ordem em que multiplicamos não altera o resultado.
Existência de elemento neutro
Na multiplicação, o 1 é o elemento neutro. Isso significa que, ao realizar a multiplicação de um número por 1, o resultado será o próprio número:
a×1 = a
Exemplo:
5 × 1 = 5
Existência de um inverso
Dado um número a, diferente de zero, existe um número em que, ao multiplicá-lo por a, o produto será o elemento neutro.
![]()
Jogo de sinal
Quando realizamos a multiplicação entre números inteiros, é interessante conhecer o jogo de sinal, para saber qual será o sinal do produto. Quando multiplicamos dois números com sinais iguais, a resposta é sempre positiva; quando os números possuem sinais opostos, o produto é sempre negativo. Para facilitar, veja a tabela com o jogo de sinal:
Sinal do primeiro fator |
| Sinal do segundo fator |
| Sinal do produto |
+ | × | + | = | + |
– | × | – | = | + |
+ | × | – | = | – |
– | × | + | = | – |
Exemplo:
a) – 4 × 5 = – 20
b) 4 × (– 5) = – 20
c) 4 × 5 = 20
d) – 4 × (– 5) = 20
Exercícios resolvidos
Questão 1 – Em uma sala de espera, há 4 fileiras com 5 cadeiras cada e 6 fileiras com 4 cadeiras cada. Sendo assim, o número total de cadeiras que há nessa sala de espera é:
A) 20.
B) 24.
C) 30.
D) 34.
E) 44.
Resolução
Alternativa E.
Para encontrar o número de cadeiras, vamos multiplicar a quantidade de cadeiras e a quantidade de fileiras, então:
4 × 5 + 6 × 4
20 + 24
44
Questão 2 — A imprudência no trânsito acontece devido a vários fatores, e um deles é o uso excessivo de celular. Pesquisas recentes apontam que os fatores humanos que causam acidentes são o excesso de velocidade, a embriaguez ao volante e o uso do celular ao volante. Na região metropolitana de Goiânia, capital de Goiás, o governo registrou que aconteciam, em média, 43 acidentes de trânsito por dia. Supondo que essa estatística se mantenha durante o ano posterior à pesquisa, então o número de acidentes registrado no mês de fevereiro, sabendo que esse ano não é bissexto, é igual a:
A) 1118.
B) 1204.
C) 1247.
D) 1290.
E) 1333.
Resolução
Alternativa B.
Sabemos que o mês de fevereiro, em um ano não bissexto, possui 28 dias. Se, para cada dia, são 43 acidentes de trânsito, então vamos calcular o produto da multiplicação
Fonte:https://brasilescola.uol.com.br



Comentários
Postar um comentário